Une partie réservée aux quadrilatères en géométrie. Définitions et première propriétés des quadrilatères les plus importants : le carré, le rectangle et le losange.
1 - Définition du quadrilatère
Définition
Quadrilatère
Un quadrilatère est une figure géométrique à quatres côtés et donc quatre angles. Chaque sommet est marqué d'un point.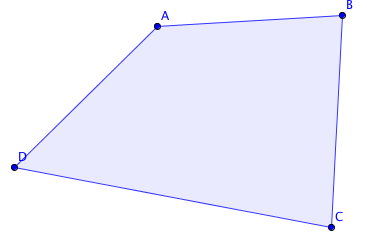
Ici, c'est le quadrilatère ABCB, de côtés [AB], [BC], [CD] et [DA] et les angles
 ,
,  ,
,  et
et  .
.
Remarque
On peut nommer le quadrilatère de plusieurs façons différente : ABCD ou DCDA ou DABC, du moment que l'ordre des lettre suivent le sens du quadrilatère.
On ne peut pas l'appeler ABDC par exemple, parce-qu'il serait croisé.
On ne peut pas l'appeler ABDC par exemple, parce-qu'il serait croisé.
2 - Carré
Définition
Carré
Un carré est un quadrilatère à quatre côtés égaux et quatre angles droits.
Ici, le quadrilatère ABCB est un carré, avec AB = BC = CD = DA et les angles
 =
=  =
=  =
=  = 90°.
= 90°.
Un carré est à la fois un rectangle et un losange, que nous allons voir tout de suite.
3 - Rectangle
Définition
Rectangle
Un rectangle est un quadrilatère dont les côtés sont égaux deux à deux et quatre angles droits.
Ici, le quadrilatère ABCB est un rectangle, avec AB = CD et BC = DA et les angles
 =
=  =
=  =
=  = 90°.
= 90°.
4 - Losange
Définition
Losange
Un losange est un quadrilatère à quatre côtés égaux et dont les diagonales se coupent perpendiculairement.
Ici, le quadrilatère ABCB est un losange, AB = BC = CD = DA et diagonales [AC] et [BD] se coupent en angle de 90°..



