Les figures géométriques tels que le segment, la droite, l'angle ou le cercle, possèdent des symétriques par une symétrie axiale, mais lesquels ? C'est ce que nous verrons dans ce cours.
1 - Propriété de la symétrie axiale
Voici la propriété fondamentale de la symétrie axiale.
Propriété
Conservation par symétrie axiale
La symétrie axiale conserve les longueurs et les mesures des angles.En gros, la symétrie axiale ne déforme pas les "objets" transformés.
2 - Image d'un segment
Voyons ce que devient l'image d'un segment par une symétrie axiale.
Propriété
Image d'un segment
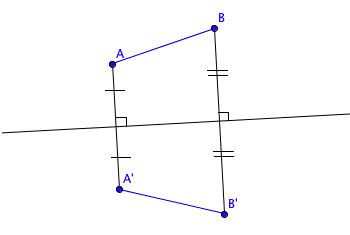
L'image d'un segment par une symétrie axiale est un segment.Pour construire son image, on construit les images de ses deux extrémités. En reliant ces deux images de points, on obtient l'image du segment.
Exemple
3 - Image d'une droite
Voyons à présent ce que devient l'image d'une droite par une symétrie axiale.
Propriété
Image d'une droite
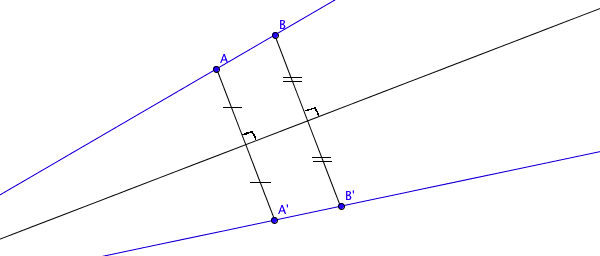
L'image d'une droite par une symétrie axiale est une droite.Pour construire son image, on prend deux points de la droites et on construit les images de ses deux points. En reliant ces deux images de points, on obtient l'image de la droite.
Exemple
4 - Image d'un angle
Vous l'avez compris, c'est toujours pareil.
Propriété
Image d'un angle
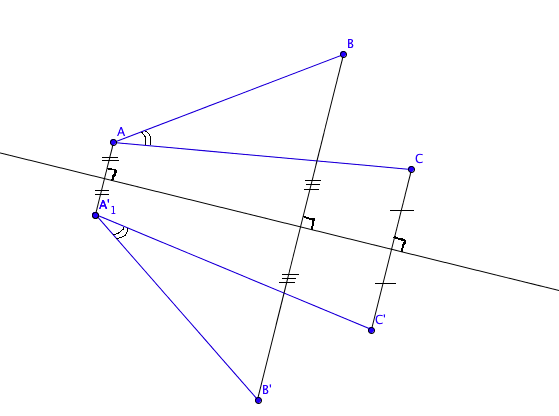
L'image d'un angle par une symétrie axiale est un angle de même mesure.Pour construire son image, on construit les images des trois points qui constituent l'angle. En reliant ces images de points dans le bon ordre, on obtient l'image de l'angle.
Exemple
5 - Image d'un cercle
L'image d'un cercle pour finir.
Propriété
Image d'une cercle
L'image d'un cercle par une symétrie axiale est un cercle de même rayon.Pour construire son image, on construit l'image de son centre et on prend un point du cercle et on construit également son image. En reliant les deux images de points, on obtient le rayon de l'image du cercle. On a plus qu'à tracer le cercle.
Exemple





