Après le théorème de Thalès, sa réciproque. Ce cours sur la réciproque du théorème de Thalès est une nouveauté cette année. C'est simplement le chemin inverse de ce fameux théorème de géométrie.
Voici la nouveauté de cette année. On va apprendre à utilisé le théorème de Thalès mais à l'envers.
Théorème
Réciproque du théorème de Thalès
On considère deux triangles, OAB et ORS, qui ont un sommet commun, le point O.

Si :
Alors, les droites (AB) et (RS) sont parallèles.

Si :

Alors, les droites (AB) et (RS) sont parallèles.
Cette fois ci, on a toujours les deux triangles au sommet commun oui, mais on va cherché à calculer les deux rapports pour démontrer ou pas le parallélisme des deux droites. Si ces rapports sont égaux, les droites sont parallèles, sinon elles ne le sont pas.
Remarque
On va calculer les rapport des côtés qui ne sembles pas parallèles.
Exemple
On considère la figure suivantes :
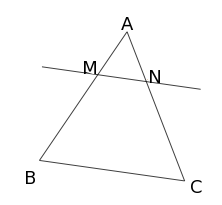
On a : AM = 45, AB = 65, AN = 54 et AC = 78.
Les droites (MN) et (BC) sont-elles parallèles ?
Pour cela, calculons les rapports des côtés qui ne sont pas parallèles.

On remarque que :
Donc, d'après la réciproque du théorème de Thalès, les droites (MN) et (BC) sont parallèles.

On a : AM = 45, AB = 65, AN = 54 et AC = 78.
Les droites (MN) et (BC) sont-elles parallèles ?
Pour cela, calculons les rapports des côtés qui ne sont pas parallèles.

On remarque que :

Donc, d'après la réciproque du théorème de Thalès, les droites (MN) et (BC) sont parallèles.
Remarque
Si on avait trouver deux rapports différents, les droites n'auraient pas été parallèles d'après le théorème de Thalès et non pas sa réciproque.
Quelques exercices sur Réciproque du théorème de Thalès :