Et si on sommait deux vecteurs ? C'est le but de ce cours sur la somme de vecteurs en introduisant une propriété fondamentale sur les vecteurs : la relation de Chasles.
On peut bien évidemment sommer deux vecteurs.
Propriété
Somme de vecteurs
La composée de deux translations de vecteurs et
et  est une translation de vecteur
est une translation de vecteur  +
+  .
.
Exemple
Dans la figure suivante,
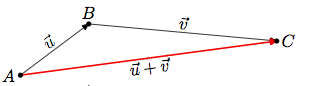
On transforme le point A en point B par la translation de vecteur .
.
Puis, le point B en point C par la translation de vecteur .
.
Donc, le point C est l'image du point A par la translation de vecteur +
+  .
.

On transforme le point A en point B par la translation de vecteur
 .
.
Puis, le point B en point C par la translation de vecteur
 .
.
Donc, le point C est l'image du point A par la translation de vecteur
 +
+  .
.
Une relation appelée Relation de Chasles traduit cela.
Propriété
Relation de Chasles
Si M' est l'image de M par la translation de vecteur et M'' l'image de M' par la translation de vecteur
et M'' l'image de M' par la translation de vecteur  , alors M'' est l'image de M par la translation de vecteur
, alors M'' est l'image de M par la translation de vecteur  +
+  et on a la relation, appelée relation de Chasles, suivantes :
et on a la relation, appelée relation de Chasles, suivantes :
 =
=  +
+ 
En fait, on a décomposé le vecteur  par M'.
par M'.
Vous remarquerez que le point d'arrivée du vecteur  est le point de départ du vecteur
est le point de départ du vecteur  . Et si l'on prend le point de départ du vecteur
. Et si l'on prend le point de départ du vecteur  et le point d'arrivée du vecteur
et le point d'arrivée du vecteur  on obtient le vecteur
on obtient le vecteur  .
.
Il y a deux méthodes de construction :
- En mettant les vecteurs bout à bout comme ceci :
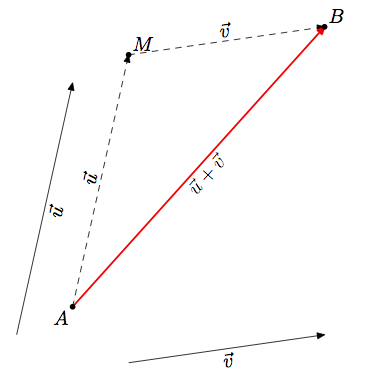
On construit le point M tel que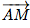 =
=  .
.
Puis on reproduit le vecteur au point M.
au point M.
Le point d'arrivée est le point B, image du point A par la translation de vecteur +
+  .
. - En utilisant les égalité du parallélogramme.

On reproduit les vecteurs et
et  au point A, ce qui nous donne respectivement les points M et N.
au point A, ce qui nous donne respectivement les points M et N.
On construit le point B tel que le quadrilatère ANBM soit un parallélogramme.