Vous connaissez ce mot 'pyramide'. Oui, c'est pareil que celles des égyptiens. Je vais vous donner tout un tas de vocabulaire sur les pyramides, son patron et la formule pour calculer son volume.
Commençons par étudier la pyramide avec tout d'abord la définition puis le patron et on terminera avec son volume.
Définition de la pyramide
Vous savez ce qu'est une pyramide égyptienne ? Donc vous connaissez la définition que je vais vous apprendre tout de suite.
Définition
Pyramide
Une pyramide est constituée d'une base polygonale et de faces latérales triangulaires.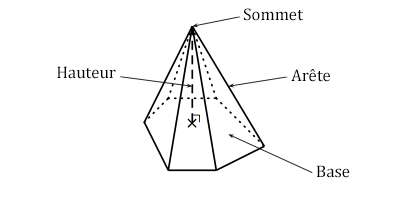
Les triangles des faces latérales ont un sommet commun que l'on appelle le sommet de la pyramide, leurs côtés sont les arêtes de la pyramide.
On appelle hauteur de la pyramide, le segment perpendiculaire à la base issu du sommet.
Un peu de vocabulaire à apprendre, mais à part cela, ça reste la pyramide égyptienne que vous connaissiez. Sauf que la pyramide égyptienne n'a souvent que 4 faces latérales.
Remarque
De plus, lorsque la base est un triangle, la pyramide est appelée tétraèdre. N'importe quel triangle peut alors être considéré come la base.
Patron de la pyramide
Je vous rappelle que le patron est une représentation à plat d'une figure 3D . En la dépliant suivant ses faces, on obtient cette figure en 3 dimensions.
Définition
Patron de la pyramide
Le patron d'une pyramide est formé de triangles correspondant à ses faces latérales, ainsi que d'un polygone correspondant à sa base.Exemple

Volume de la pyramide
Comme toute figure en 3 dimensions, elle possède un volume. Je vous donne ici la formule du volume d'une pyramide.
Propriété
Volume de la pyramide
Le volume d'une pyramide s'obtient en multipliant l'aire d'une base par la hauteur en divisant le tout par 3 :
Il faut donc connaître ses formules d'aires pour calculer le volume d'une pyramide.
Vous avez dû el remarquer, c'est le volume d'un prisme droit, divisé par 3.
Exemple

L'aire de la base, qui est un carré, vaut :
La hauteur vaut, quant à elle :
Donc, le volume de cette pyramide vaut :

Remarque
L'unité quant à elle, est celle de la longueur est côtés de la pyramide.
Quelques exercices sur Pyramide :