Le cours sur le théorème de Thalès en 4ème. Théorème fondamental de la géométrie, il généralise les théorèmes des milieux vus dans la partie précédente.
Vous allez adorer ce théorème, j'en suis sûre.
Théorème
Théorème de Thalès
On considère deux triangles, OAB et ORS, qui ont un sommet commun, le point O. De plus, les droites (AB) et (RS) sont parallèles.

On a alors les relations d'égalité suivantes :
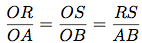

On a alors les relations d'égalité suivantes :
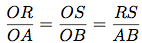
Comprennez bien ces formules. Prenons par exemple le côté [OA]. On a R ∈ [OA]. On fait le petit sur le grand à chaque fois, le sommet commun jusqu'au point R sur le sommet commun jusque l'autre point, le point A, soit : 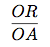
On peut aussi faire le grand sur le petit. Quoi qu'on fasse comme fraction, on le fait dans toute l'égalité.
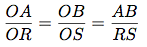
Remarques
- Lorsque l'on fait sur les côtés qui ne sont pas parallèles, on a toujours en commun au numérateur et au dénominateur des fractions le point O, somme commun des deux triangles.
- On peut également appliquer le théorème de Thalès dans le cas de figure suivant :
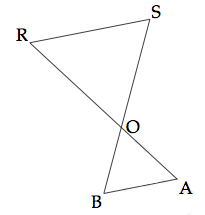
On a bien deux triangles, OAB et ORS, qui ont un sommet commun, le point O et les droites (AB) et (RS) sont parallèles.
Exemple
On considère la figure suivante. On suppose que (AB) // (CD).
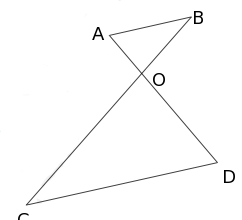
On donne : AO = 2cm, BO = 3cm, CO = 6cm et CD = 8cm.
Calculer AB.
Je vais vous donner la correction type à adapter à chaque fois que vous serez confronté à cette situation. Tachez de la reproduire au mot près.
On considère les triangles ABO et CDO de sommet commun O.
De plus, d'après l'énoncé, les droites (AB) et (CD) sont parallèles.
Nous avons toutes les conditions requises pour appliquer le théorème de Thalès.
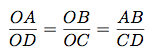
On va prendre deux fractions dont une que l'on connait entièrement et l'autre où l'on connait une valeur et l'autre est la valeur recherchée.
La fraction OB/OC est entièrement connue car BO = 3cm et CO = 6cm, on la garde.
On veut calculer AB et l'on connait CD, prenons donc AB/CD.
On a donc :
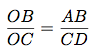
Isolons la valeur que l'on veut calculer, c'est-à-dire AB, en faisant passé le CD du dénominateur de droite au numérateur de gauche.
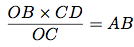
On fait l'application numérique en utilisant les valeurs données dans l'énoncé.
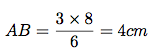
Nous avons terminé l'exercice.
Cela peut parraîttre long, mais c'est parce-que j'ai bien prix mon temps pour tout vous expliquer.

On donne : AO = 2cm, BO = 3cm, CO = 6cm et CD = 8cm.
Calculer AB.
Je vais vous donner la correction type à adapter à chaque fois que vous serez confronté à cette situation. Tachez de la reproduire au mot près.
On considère les triangles ABO et CDO de sommet commun O.
De plus, d'après l'énoncé, les droites (AB) et (CD) sont parallèles.
Nous avons toutes les conditions requises pour appliquer le théorème de Thalès.
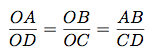
On va prendre deux fractions dont une que l'on connait entièrement et l'autre où l'on connait une valeur et l'autre est la valeur recherchée.
La fraction OB/OC est entièrement connue car BO = 3cm et CO = 6cm, on la garde.
On veut calculer AB et l'on connait CD, prenons donc AB/CD.
On a donc :
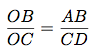
Isolons la valeur que l'on veut calculer, c'est-à-dire AB, en faisant passé le CD du dénominateur de droite au numérateur de gauche.
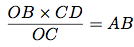
On fait l'application numérique en utilisant les valeurs données dans l'énoncé.
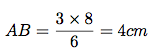
Nous avons terminé l'exercice.
Cela peut parraîttre long, mais c'est parce-que j'ai bien prix mon temps pour tout vous expliquer.
Quelques exercices sur Théorème de Thalès :