On débute ce cours par les parallélépipèdes rectangles. Je vais vous définir d'abord ce que c'est, avant de les étudier, notamment leurs volumes.
On commence donc par le parallélépipède rectangle. Mais avant tout, savez-vous ce que c'est ? Ne vous inquiètes pas, je vais vous le définir de suite.
Définition du parallélépipède rectangle
Voici la définition du parallélépipède rectangle.
Définition
Parallélépipède rectangle
Un parallélépipède rectangle est un solide composé de 6 faces rectangulaires toutes perpendiculaires entre elles.Il possède 8 sommets et 12 arêtes comme présentées sur la figure ci-dessous.
Parmi ses 6 faces, on distingue : 2 bases (une au dessus et une en dessous) et 4 faces latérales (sur les côtés).
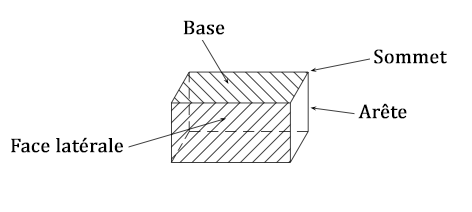
Avec la figure, cela doit sûrement être plus clair.
Vous avez tout compris ? C'est un espèce donc de gros cube rectangulaire. J'en suis sûr que vous en avez déjà vu ou même dessiné sur le coin d'un table de classe.
Par exemple, une boîte à chaussures est un parallélépipède rectangle. Ou même une armoire.
Représentation en perspective des solides
Pour représenter des solides en 3D, on utilise la perspective cavalière.
Définition
Perspective cavalière
On représente les solides en perspectives cavalières, c'est-à-dire que :- On ne dessine que les arêtes,
- Les arêtes visibles sont dessinées en trait plein,
- Les arêtes cachées sont dessinées en pointillés.

C'est pas très compliqué, posez-vous la question "que vois-je ?" et ce que je voyez, vous le dessiné en traits pleins. Le reste, pour que cela soit plus lisible, vous le dessiné en pointillés.
Bien évidement, seulement les arêtes sont représentés. En même temps, que voulez-vous représenter d'autre ?
Exemple

Que voit-on ? Eh bien toutes les arrêtes sauf [EH], [DH] et [HG] que l'on a représenté en pointillés.
Patron d'un solide
Ah ça je sais ce que c'est ! C'est le bosse ! Non ?
Pas du tout ! Si je vous parle de patron dans le chapitre sur les parallélépipèdes rectangles, vous vous doutez bien qu'il y a un lien.
En effet, je vous l'explique tout de suite dans la définition suivante.
Définition
Patron d'un solide
Le patron d'un solide est un dessin plan qui permet, une fois découpé et plié, de reconstitué le solide en 3 dimensions.
C'est quelque peu différent de votre version n'es-ce pas ?
En fait, c'est simplement un dessin sur une feuille papier pour créer un vrai parallélépipède rectangle en 3D. Vous en avez déjà dessiné, c'est certain ! Si ce n'est pas le cas, dessinez-en un grâce à l'exemple suivant, découpé-le et plier le tout, vous obtiendrez un parfait parallélépipède rectangle en 3D !
Exemple

Je veux maintenant le réalisé en 3 dimensions. Pour cela, je prend une feuille de papier et je dessine son patron, comme ceci :

Volume du parallélépipède rectangle
Ici, on va parler de volume. Qu'es-ce que le volume ? C'est en fait l'intérieur du solide.
Par exemple, le volume d'un verre, c'est combien d'eau il peut contenir si on le remplir à ras bord.
Propriété
Volume d'un parallélépipède rectangle
Soit le parallélépipède rectangle de longueur a, de largeur b et de hauteur h.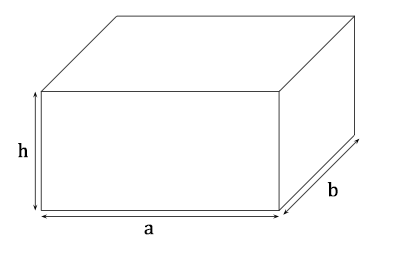
Son volume vaut :
En fait, c'est l'aire du rectangle de base multipliée par la hauteur du parallélépipède rectangle.
Remarque
Exemple
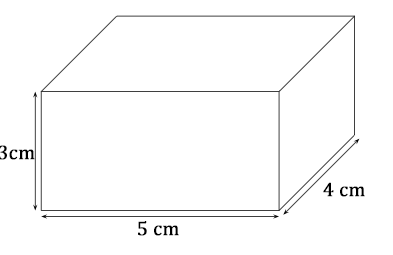
En effet :
Quelques exercices sur Parallélépipède rectangle :