Maintenant que vous connaissez tout sur les fonctions en général, nous allons les manipuler dans des opérations simples : additions, multiplication, quotient et composition de fonctions.
Nous allons voir maintenant que l'on peut effectuer des opérations sur des fonctions.
Commençons par la somme de deux fonctions.
Propriété
Addition de fonctions
Soient f et g deux fonctions définie sur I.La fonction f + g est la fonction définie aussi sur le domaine I par :
La courbe représentative de cette fonction se déduit point par point à partir de la courbe de f en ajoutant les ordonnées.
Propriétés
Addition et variations fonctions
Soient f et g deux fonctions définie sur I.- Si f et g sont deux fonctions croissantes, alors la fonction f + g est aussi une fonction croissante,
- Si f et g sont deux fonctions décroissantes, alors la fonction f + g est aussi une fonction décroissante.
Et maintenant : la multiplication d'une fonction par un réel k.
Propriété
Multiplication de fonctions par un réel
Soit f une fonction définie sur I et k ∈ .
.
La fonction kf est la fonction définie aussi sur le domaine I par :
La courbe représentative de cette fonction se déduit point par point à partir de la courbe de f en multipliant l'ordonnée f(x) par k.
Propriétés
Multiplication par un réel et variations de fonctions
Soit f une fonction définie sur I et k ∈ .
.
- Si k > 0, alors les fonctions f et kf ont le même sens de variation,
- Si k < 0, alors les fonctions f et kf ont des sens de variation opposés.
Puis le produit de deux fonctions.
Propriété
Multiplication de fonctions
Soient f et g deux fonctions définie sur I.La fonction f × g est la fonction définie aussi sur le domaine I par :
Et leur quotient.
Propriété
Quotient de fonctions
Soient f et g deux fonctions définie sur I, tel que g(x) ≠ 0 pour tout réel x.La fonction
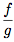 est la fonction définie aussi sur le domaine I par :
est la fonction définie aussi sur le domaine I par :
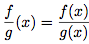
Une opération nouvelle à présent : la composition.
Propriété
Composition de fonctions
Soient f une fonction définie sur I et g(x) une fonction définie sur f(I).La fonction
 (on dit "g rond f")est la fonction définie aussi sur le domaine I par :
(on dit "g rond f")est la fonction définie aussi sur le domaine I par :

En fait, on remplace la variable de la fonction g par la fonction f.
Exemple
Si on veut
 :
:

Vous avez saisie l'idée ?
Je vous laisse terminer le calcul.
Propriétés
Composition et variations de fonctions
Soient f une fonction définie sur I et g(x) une fonction définie sur f(I).- Si f et g ont le même sens de variation, alors
 est croissante,
est croissante, - Si f et g ont des sens de variation opposés, alors
 est décroissante.
est décroissante.
Toutes ces notions sur les opérations de fonction vont vous aider à étudier les variations des fonctions.
Vous pourrez considérez que la fonction à étudier est une somme, un produit, un quotient de deux fonctions, ou alors une fonction multiplier par un coefficient (k rappelez-vous).
Vous utiliserez ainsi les propriétés que je viens de vous apprendre.
Exemple
En effet :
- La fonction carrée est croissante sur [0 ; +∞[,
- La fonction x est croissante sur [0 ; +∞[, donc la fonction 3x l'est aussi par produit de fonction par une réel,
- Par somme de deux fonctions : la fonction f(x) = x² + 3x est croissante sur [0 ; +∞[.