Ce cours de maths sur les équations cartésiennes des droites vous enseignera à déterminer une équation cartésienne d'une droite définie par un point et un vecteur directeur, entre autre.
On passe aux équations cartésiennes dans le plan.
Définition
Equation cartésienne d'une droite
Soient un repère
, a, b deux réels dont au moins un est non nul et c un réel.
Dans le repère
, toute droite admet une équation cartésienne de la forme : ax + by + c = 0.
On connaissait l'équation d'une fonction affine rappelez-vous. Bien c'est la même chose, on a juste rassemblé les x et les y ensembles.
Et bien quoi ? Oui, une fonction affine, c'est une droite !
Remarque
Une droite parallèle à l'axe des ordonnées s'écrit : x = k avec k ∈ 
.
.
Comment on détermine l'équation cartésienne d'une droite à partir de deux points ?
Suivez bien l'exemple qui suit.
Exemple
Soient A(3, 4) et B(-1, 2) deux points du plan. Déterminons l'équation cartésienne de la droite (AB).
Cet équation s'écrit : y = ax + b.
Oui, c'est une fonction affine en fait.
On a deux points donc deux équations :
Soit :
Que l'on résout aisément, en soustrayant la deuxième équation à la première.
On a donc :
.
Puis :
Soit :
.
Donc l'équation de la droite (AB) est :
Cet équation s'écrit : y = ax + b.
Oui, c'est une fonction affine en fait.
On a deux points donc deux équations :
Soit :
Que l'on résout aisément, en soustrayant la deuxième équation à la première.
On a donc :
.
Puis :
Soit :
.
Donc l'équation de la droite (AB) est :
Définitions
Vecteur directeur et vecteur normal
Soit une droite Δ d'équation ax + by + c =0.- Le vecteur
(-b, a) est un vecteur directeur de Δ. - Le vecteur
(a, b) est un vecteur normal de Δ.
Le vecteur directeur, comme son nom l'indique, dirige la droite. Tandis que le vecteur normal est perpendiculaire à la droite.
Exemple
Trouver l'équation cartésienne de la droite 
passant par le point A(5, 2) et parallèle à la droite ' d'équation x - 2y + 3 = 0.
On sait que le vecteur(2, 1) est directeur à la droite '.
Soit un point M(x, y) du plan.
Pour que ce point appartienne à la droite, il faut que les vecteurs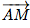 
et sont colinéaires.
En langage mathématiques, cela se traduit ainsi :
La notation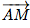 // signifie "colinéaire à". Ne mettez pas cela dans votre copie, c'est uniquement pour que vous compreniez.
Voilà, nous l'avons notre équation cartésienne.
passant par le point A(5, 2) et parallèle à la droite ' d'équation x - 2y + 3 = 0.
On sait que le vecteur
(2, 1) est directeur à la droite '.
Soit un point M(x, y) du plan.
Pour que ce point appartienne à la droite
, il faut que les vecteurs 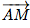et sont colinéaires.
En langage mathématiques, cela se traduit ainsi :
La notation
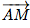// signifie "colinéaire à". Ne mettez pas cela dans votre copie, c'est uniquement pour que vous compreniez.
Voilà, nous l'avons notre équation cartésienne.
Quelques exercices sur Equation cartésienne d'une droite :