Voici un cours sur la forme canonique d'un polynôme du second degré. Je vous donne la formule à apprendre par coeur et sa démonstration, à savoir reproduire.
Et alors ? Je vais vous montrer comment trouver la forme canonique d'une expression. Suivez bien mon raisonnement, il est important que vous le compreniez.
On part du polynôme P:
On factorise ce polynôme par a.
Par a? Mais il n'est pas en facteur partout ! Comment je fais ?
Là où le a n'est pas en facteur apparant, vous diviserez par a tout simplement. Regardez :
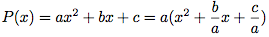
Vous voyez bien qu'en développant on retombe sur l'expression du départ.
Continuons. On ne va se préoccuper que de la partie
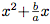en factorisant à l'aide d'une identité remarquable a² + 2ab + b² = (a + b)² comme ceci :
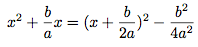
On doit enlever
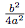car :
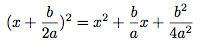
Et nous nous ne voulons que
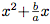. Donc la meilleure des choses à faire, c'est d'enlever .
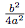Ce qui nous donne :
Mettons sous le même dénominateur les deux dernière fractions.
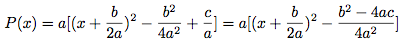
On note Δ la quantité
,
Et on a fini :
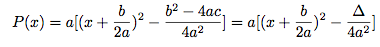
Résumons tout ça.
Propriété
Forme canonique d'un polynôme
Soit P(x) = ax² + bx + c un polynôme du second degré avec a ≠ 0.On appelle forme canonique de P :
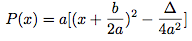
Avec Δ le discriminant de P :
Exemple
Soit le polynôme P(x) = x² + 2x - 1. Donner sa forme canonique.
On a donc ici : a = 1, b = 2 et c = -1.
On applique tout bêtement la formule :
On a :
Δ = 2² - 4 × 1 × (-1) = 8
Calculons donc la forme canonique.
On a terminé.
On a donc ici : a = 1, b = 2 et c = -1.
On applique tout bêtement la formule :
On a :
Calculons donc la forme canonique.
On a terminé.
Bien évidemment, on pourrez vous demandez de refaire le raisonnement précédent.
Quelques exercices sur Forme canonique d'un polynôme du second degré :