Fonctions trigonométriques : fonction sinus et fonction cosinus

Les fonctions trigonométriques ne seront pas vos favorites. Nous étudierons dans ce cours les fonctions cosinus et sinus et quelques notions trigonométriques en bonus.

Cette fois-ci, une grande concentration est demandée car les fonction trigonométriques sont ultra importantes en mathématiques.
Nous allons d'abord introduire quelques notions, avant de les étudier.

Définition

Cercle trigonométrique

Soit un repère orthonormal (O ; I ; J). On appelle cercle trigonométrique le cercle de centre 0, de rayon 1, orienté dans le sens positif (ou sens direct).

Remarque

Attention, le sens positif est le sens contraire au aiguilles d'une montre. Ne me demandez pas pourquoi, c'est une convention mathématiques.

Définitions

Fonctions trigonométriques

Soit un repère orthonormal (O ; I ; J).
On appelle cosinus de x, noté cos x, l'abscisse du point M appartenant au cercle trigonométrique, et sinus de x, noté sin x, l'ordonnée de ce point M.

cercle trigonométrique cosinus et sinus

Mais ce ne sont pas des fonctions si elles sont sur un cercle ? Je n'ai pas compris.

Si, ce sont des fonctions que l'on représente sur un cercle. Je vous les présente dans un "vrai" repère tout de suite.

Définitions

Fonction sinus et cosinus

La fonction cosinus est la fonction f définie sur par f(x) = cos x.
C'est une fonction paire et périodique de période 2π, c'est-à-dire qu'elle se répète tous les 2π.
Sur une période [-π; π], elle est croissante sur [-π ; 0] et décroissante sur [0 ; π].
La courbe représentative de la fonction cosinus est une sinusoïde.

La fonction sinus est la fonction f définie sur par f(x) = sin x.
C'est une fonction impaire et périodique de période 2 π.
Sur une période [-π; π], elle est décroissante sur [-π ; -π/2] et sur [π/2; π] et croissante sur [-π/2 ; π/2].
La courbe représentative de la fonction sinus est une sinusoïde.

Il existe un tas de propriétés pour ces deux fonctions sin et cos. En voici quelques-unes.

Propriétés

Propriétés des fonction trigonométriques

Voici les deux principales propriétés des fonctions cosinus et sinus.

Pour tout réel x : -1 ≤ cos x ≤ 1 et -1 ≤ sin x ≤ 1.

cos² x+ sin² x = 1

Parité : cos(-x) = cos (x) (fonction paire) et sin(-x) = -sin (x) (fonction impaire).

Remarque

Quand on dit "π", "π/2", etc. on parle de radians. Sachez que 2π radians vaut 360°.

Exemple

60° vaut π/3 radians.
En effet, par le produit en croix :

fonction trigonométriques

Il y a des valeurs à connaître par coeur, comme par exemple : valeurs des fonctions trigonométriques . Voici la suite.

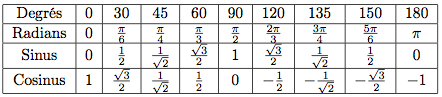
tableau de valeurs des fonctions trigonométriques

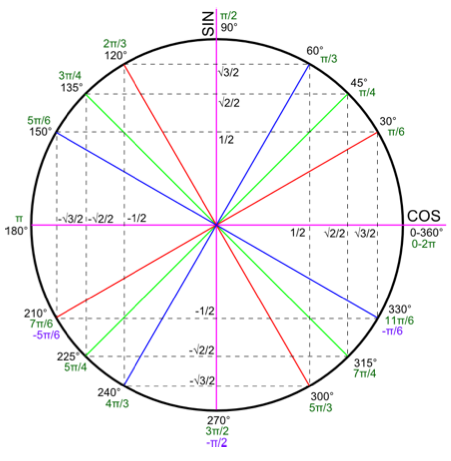
Et comment je fais pour les autres angles ?

Vous vous servirez des propriétés de parités ou autres pour les déterminer. Ou utilisez la remarque suivante.

Remarque importante

Pour donner la valeur principale d'un angle, on décomposera sous la forme θ + 2kπ, avec θ appelée mesure principale de l'angle.

Exemple 1

Donner la valeur de

.
On décompose le etude de fonction trigonométriques

comme ceci :

étude de fonction cosinus

Or, cos(4π) = 0.
Donc :

étude de fonction sinus

Exemple 2

Sachant que x est dans une premier quart du cercle trigonométrique, et que étude de fonction trigo

, calculer sin x.
On sait que, pour tout x, cos² x + sin² x = 1, donc :

fonction trigo

Donc :

Or, x se trouve dans le premier quart du cercle trigonométrique, là où le sinus est positif. Donc :

Avec la calculatrice, on trouve une valeur approchée de x à 10^-3 près de : x = 0,841 rad.