La suite (un) est définie pour n ≥ 1 par :
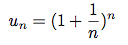 .
.
Le but de cet exercice est de déterminer la limite de cette suite.
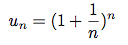 .
.Le but de cet exercice est de déterminer la limite de cette suite.
-
Montrer que, pour tout réel x, on a : 1 + x ≤ ex.
En déduire que si n ≥ 1, alors ≤ e.
≤ e.On sait que 1 + x ≤ ex (cela se démontre très facilement).
En posant x = 1/n, on a : si n ≥ 1, alors :1 + 1/n ≤ e1/n
Donc, la fonction xn, n naturel non plus, étant croissant sur [0; +∞[ :(1 + 1/n)n ≤ e -
En posant X = -x, montrer que si X < 1, alors
 ≤
≤  .
.
En déduire que si n ≥ 1, alors e ≤ .
.On pose X = -x.
Si X < 1, alors 0 < 1 - X - e-X et donc :
Or : X = 1/(n + 1) donne :
Et :
En utilisant la question précédente, on obtient :
-
En déduire que si n ≥ 1, alors 0 ≤ e - un ≤ 3/n.
D'après les questions précédentes, pour tout n ≥ 1 :

Donc :
Or :
Donc :
-
En conclure que :
 .
.On a :

Donc :
D'où :