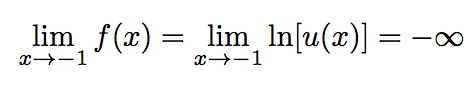Déterminons tout d'abord l'ensemble de définition de cette fonction f.
Cette fonction est définie lorsque 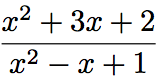 > 0 car un logarithme ne "mange" que du positif".
> 0 car un logarithme ne "mange" que du positif".
Le discriminant du polynôme du dénominateur est négatif, ce qui signifie qu'il est toujours positif : x² -x + 1 > 0.
Les racines du polynôme du numérateur x² + 3x + 2 sont -1 et -2.
En traçant le tableau de signes de ce polynôme, on trouve que :
Et comme le dénominateur est toujours positif,
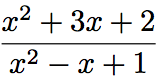 > 0 ⇔ x ∈ ]-∞; -2;[U]-1; +∞[
> 0 ⇔ x ∈ ]-∞; -2;[U]-1; +∞[
D'où : Df = ]-∞;-2[U]-1; +∞[.
On peut à présent revenir au calcul des limites.
Prenons u(x) =
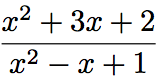 tel que f(x) = ln[u(x)].
tel que f(x) = ln[u(x)]. Réécrivons la fonction u de cette façon :
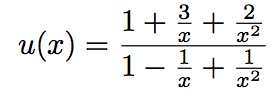
On a :
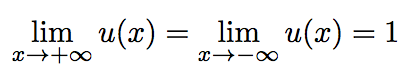
De plus,
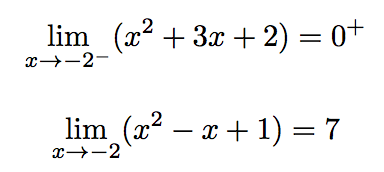
Donc :
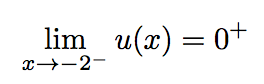
Et :
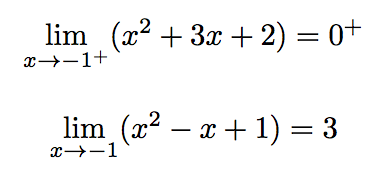
Donc :
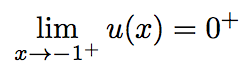
Limite en ±∞ :
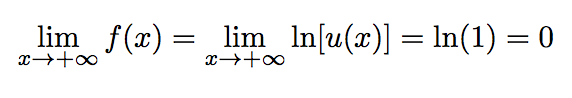
Limite en -2 :
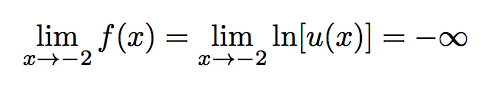
Limite en -1 :