Calculons d'abord les coordonnées des vecteurs  et
et  .
.
 (0; -5; 0) et
(0; -5; 0) et  (1; -3; -3).
(1; -3; -3).
Cela se voit très bien que ces deux vecteurs ne sont pas colinéaires.
Donc, les points A, B et C ne sont aps alignés.
Pour déterminer une équation cartésienne du plan P passant par ces points, on va prendre un vecteur  de l'espace. Cela va être un vecteur normal au plan (ABC).
de l'espace. Cela va être un vecteur normal au plan (ABC).
Calculons ses coordonnées.
 .
. = 0 ⇔ -5b = 0
= 0 ⇔ -5b = 0
 .
. = 0 ⇔ a - 3b - 3c = 0
= 0 ⇔ a - 3b - 3c = 0
Ce qui nous permet de trouver :
a = 3c
Donc, comme vecteur normal au plan (ABC), on peut prendre
 (3; 0; 1).
(3; 0; 1).
Soit donc un point M(x; y; z) quelconque de l'espace.
Ce point M apparatient au plan (ABC) si et seulement si
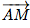 et
et  sont orthogonaux, c'est-à-dire si le produit scalaire de ces deux vecteur est nul.
sont orthogonaux, c'est-à-dire si le produit scalaire de ces deux vecteur est nul.
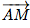 .
. = 0
= 0
⇔ 3(x - 2) + (z - 1) = 0
⇔ 3x + z- 7 = 0
Donc, une équation cartésienne du plan (ABC) est :