Les trois questions suivantes sont indépendantes.
-
Soient les points de l'espace A(1; 2; 3) et B(3; -1; 2).
Déterminer une équation de la sphère (S) de diamètre [AB].Soit M(x; y; z) un point de l'espace.
Ce point M appartient à la sphère recherchée si, et seulement si, les vecteurs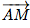 et
et  sont orthogonaux, autrement dit si leur produit scalaire est nul.
sont orthogonaux, autrement dit si leur produit scalaire est nul.
M ∈ (S) ⇔ 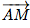 .
. = 0
= 0
M ∈ (S) ⇔ (x - 1)(x - 3) + (y - 2)(y + 1) + (z - 3)(z - 2) = 0
M ∈ (S) ⇔ x² + y² + z² - 4x - y - 5z + 7 = 0
Donc, l'équation de la sphère (S) de diamètre [AB] est :
x² + y² + z² - 4x - y - 5z + 7 = 0 -
Déterminer une équation de la sphère (S)' de centre Ω(1; 2; 3) et de rayon 2.
Soit M(x; y; z) un point de l'espace.
Ce point M appartient à la sphère recherchée si, et seulement si, le rayon du cercle ΩM = 2.
M ∈ (S) ⇔ ΩM = 2
M ∈ (S) ⇔ ΩM² = 4
M ∈ (S) ⇔ (x - 1)² + (y - 2)² + (z - 3)² = 4
M ∈ (S) ⇔ x² + y² + z² - 2x - 4y - 6z + 10 = 0
Donc, l'équation de la sphère (S)' de centre Ω(1; 2; 3) et de rayon 2 est :
x² + y² + z² - 2x - 4y - 6z + 10 = 0 -
Déterminer une équation de la sphère (S)'' de centre Ω(1; 2; 3) et tangente au plan d'équation 2x - y + z + 2 = 0.
Déterminons dans un premier temps la distance r du point Ω au plan d'équation 2x - y + z + 2 = 0.
r = |2 × 1 - 2 + 3 + 2| = 5 √2² + (-1)² + 1² √6
Soit M(x; y; z) un point de l'espace.
Ce point M appartient à la sphère recherchée si, et seulement si, le rayon du cercle ΩM vaut 5/√6.
M ∈ (S) ⇔ ΩM = 5 √6
M ∈ (S) ⇔ (x - 1)² + (y - 2)² + (z - 3)² = 25 6
M ∈ (S) ⇔ x² + y² + z² - 2x - 4y - 6z - 59 = 0 6
Donc, l'équation de la sphère (S)'' de centre Ω(1; 2; 3) et tangente au plan d'équation 2x - y + z + 2 = 0 est :
x² + y² + z² - 2x - 4y - 6z - 59 = 0 6