Soient, dans le plan, les points A(2; 3) et B(3; -1).
-
Déterminer une équation du cercle C de diamètre [AB].
Soit un point M(x; y). On obtient une équation du cercle C en disant (par exemple) que les vecteurs
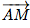 et
et  sont orthogonaux, c'est-à-dire que leur produit scalaire est nul.
sont orthogonaux, c'est-à-dire que leur produit scalaire est nul.
M(x; y) ∈ (C) ⇔ 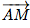 .
. = 0
= 0
⇔ (x - 2)(x - 3) + (y - 3)(y + 1) = 0
⇔ x² - 5x + y² - 2y + 3 = 0 -
Vérifier que le point C(2; -1) appartient au cercle C.
Le point C appartient au cercle C car ses coordonnées vérifient parfaitement l'équation du cercle.
-
Donner une équation de la tangente au cercle au point C.
Notons Ω le centre du cercle (C) et (T) la tangente au point C.
Ω est donc le milieu de [AB], il a donc pour coordonnées (5/2; 1).
Reprenons toujours ce fameux point M(x; y). On obtient une équation de la tangente au cercle au point C en disant que les vecteurs et
et  sont orthogonaux, autrement dit : que leur produit scalaire est nul.
sont orthogonaux, autrement dit : que leur produit scalaire est nul.
M(x; y) ∈ tT) ⇔  .
. = 0
= 0
⇔ (x - 2)(-1/2) + (y + 1)(-2) = 0
⇔ x + 4y + 2 = 0