Un cours sur les vecteurs avec au programme : définition, propriétés, vecteurs égaux et opposés et une partie qui reprend la notion de translation en la mêlant avec les vecteurs.
1 - Définition des vecteurs
Qu'es-ce qu'un vecteur ? Commençons par là.
Définition
Vecteur
Un vecteur est défini par trois choses :- Une direction,
- Une longueur,
- Un sens.
On a souvent tendance à marqué un vecteur par deux points, un de départ et un point d'arrivé :
.
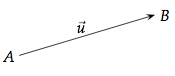
Dans la figure précédente, c'est une translation de vecteur qui transforme le point A en B, ainsi que tous les autres points de la figure 
par les points correspondant de la figure ' tel que chaque point et son image soit translatés d'une même longueur, d'un même sens et d'une même direction que le vecteur .
2 - Vecteurs égaux
Lorsqu'on translate une figure, on translate en fait tous les points qui composent cette figure. Et ces points et leurs images correspondantes forment chacun un vecteur égal au vecteur de la translation.
Définition
Vecteurs égaux
Si deux vecteurs ont la même direction, la même longueur et le même sens, alors ces vecteurs sont égaux.
Regardez la figure suivante.
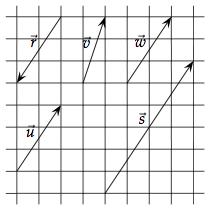
Les vecteurs
et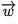 
ont la même direction mais des longueurs différentes. Ils ne sont donc pas égaux.
Tandis que les vecteurs
et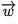 ont la même direction, le même sens et la même longueur, ils sont égaux. : = .
3 - Vecteurs opposés
S'il manque une des trois condition, c'est fichu. Par exemple, si le sens est inversé...
Définition
Vecteurs opposés
Si deux vecteurs ont la même direction, la même longueur mais le sens inverse, alors ces vecteurs sont opposés.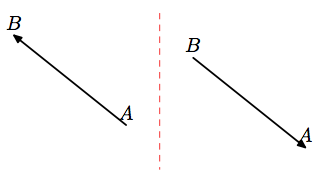
Ci-dessus, les vecteurs et 
sont opposés : = -.
4 - Vecteur nul
Le fameux vecteur nul. Vous croyez peut-être qu'il ne sert à rien. Détrompez-vous.
Mais à votre avis, c'est quoi, le vecteur nul ?
Définition
Vecteur nul
Un vecteur qui n'a ni de direction, ni de sens, ni de longueur est un vecteur nul.Exemple
et 
sont nuls car le point de départ du vecteur est le même que celui de l'arrivée.
Remarque
est nul, alors les points A et B sont confondus.
5 - Vecteurs et translation
Revenons à la translation par un vecteur.
Propriété
Vecteurs et translation
Soit un vecteur quelconque.
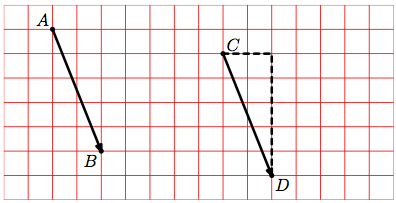
L'image du point C par la translation de vecteur
est le point D tel que : = 
.
Il existe une autre méthode lorsque cela devient plus compliqué de tracé l'image d'un point par la translation vectorielle. Nous allons le voir tout de suite.