Un cours sur la rotation dans lequel je vous définit cette nouvelle notion et vous donne les premières propriétés pour que vous réussissiez votre Brevet à la fin de l'année.
1 - Définition de la rotation
Je vous ai dis que c'était une transformation déjà. Vous ne voudriez surement pas vous contenter que de cela. Voici une définition plus complète.
Définition
Rotation
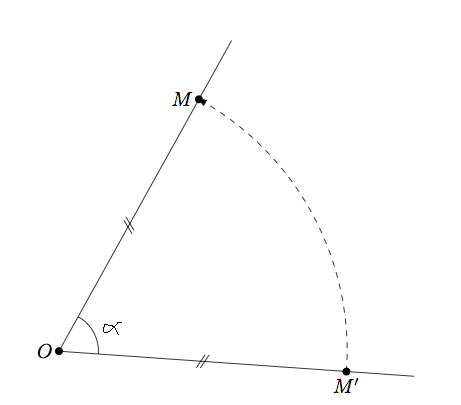
Une rotation est une transformation géométrique définie par :- un point : le centre de rotation,
- un angle,
- un sens de rotation, positif ou négatif.
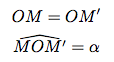
Remarque
2 - Propriétés de la rotation
Voilà les propriétés sur les rotations.
Propriétés
Propriétés de la rotation
Soient A, B, C et D quatre points du plan, et A', B', C' et D' leurs images respectives par une rotation.- La rotation conserve les longueurs: A'B' = AB ou B'C' = BC.
- La rotation conserve les angles :
 .
. - La rotation conserve les aires : le quadrilatère A'B'C'D' a la même aire que le quadrilatère ABCD.
- La rotation conserve l'alignement : si A, B et C sont alignés, alors leurs images A', B' et C' le sont aussi.
- La rotation conserve les milieux : si I est le milieu du segment [DC], alors on aura I' milieu du segment [D'C'].
- La rotation transforme un segment en un segment, une droite en une droite, une demi-droite en une demi-droite et un cercle en un cercle.
Cela se comprend très bien. C'est un peut comme la symétrie centrale. On a un point qui est le centre de rotation et au lieu de faire une symétrie, on tourne par rapport à lui, sans toucher à la figure (segment, droite, cercle ou autres). Donc, rien ne change.
Pour la construction maintenant.
Pour transformer un segment par une rotation, on transforme les deux extrémités de ce segment.
Pour transformer une drotie par une rotation, on prend deux points de cette droite et on les transforme, ce qui nous donne une nouvelle droite image de la première par cette rotation.
Pour une demi-droite, on prend l'extrémité et on choisit un second point et c'est gagné.
Quelques exercices sur Rotation :