Voici un cours sur les relations de trigonométrie dans le triangle rectangle. Vous apprendrez à calculer un angle à partir de deux côtés et inversement.
Il faut savoir tout d'abord que ces relations ne s'utilisent que dans un triangle rectangle.
Propriétés
Relations de trigonométrie dans un triangle rectangle
Soit ABC un triangle rectangle en A.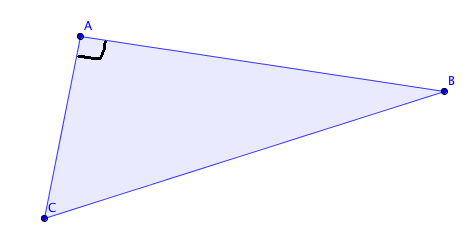
On a les relations suivantes :
Relation du sinus :
Relation du cosinus :
Relation de la tangente :
Explications : Prenons l'angle 
. Son côté adjacent est [AB] et son côté opposé est [AC].
L'hypoténuse du triangle est toujours la même. Ici, dans le triangle ABC rectangle en A, c'est le côté [BC]. C'est en fait le côté opposé à l'angle droit.
Exemple d'application
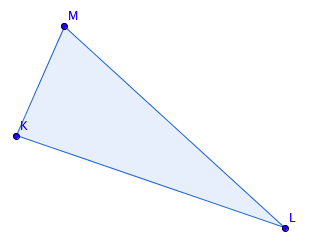
Soit le triangle KLM, rectangle en K.
On nous donne :
= 63° et KM = 4cm.
On doit calculer les deux autres côtés du triangles : LM et LK. Alors allons-y !
On commence toujours par dire qu'on a un triangle rectangle : le triangle KLM est rectangle en K.
On va donc chercher la relation trigonométrique dont on connait déjà deux termes pour l'appliquer.
On a donc la relation de trigonométrie suivante :
Or, on connait l'angle
= 63° et on connait le côté KM = 4cm. On remplace.
Et on résoud pour trouver l'hypoténuse LM. On fait donc passer le cos au dénominateur du côté droit, et l'inconnue LM à gauche.
Remarque
Quand on fait des calculs avec de la trigonométrie, on trouvera toujours un résultat approximatif. On utilise le signe ≈ au lieu du signe égal = habituel.
Quelques exercices sur Relations de trigonométrie :