Triangle isocèle, triangle équilateral et triangle rectangle

Il existe plusieurs triangles particuliers en fonction de la longueur de leurs côtés ou de la mesure de leurs angles. En effet, il y a des triangles qui ont deux côtés, d'autres dont les trois côtés sont égaux, etc. Je vais vous les énoncer dans cette partie.

Triangle isocèle

On commence par le triangle isocèle. Encore une fois, essayons de décortiquer le mot "isocèle". Il est composé de "iso" qui signifie "égal"... Vous avez trouvé ?

Définition

Triangle isocèle

Un triangle isocèle est un triangle qui possède deux côtés de même longueur.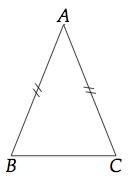



Dans le triangle ci-dessus, les côtés [AB] et [AC] sont égaux. De plus, on dit que le triangle ABC est isocèle en A. La base principale de ce triangle est le côté opposé à A, soit [BC].

Donc, deux angles égaux pour le triangle isocèle. Et les angles ?

Propriétés

Propriétés du triangle isocèle

Deux propriétés importantes sur les triangles isocèles :

• Les deux angles de la base principale d'un triangle isocèle sont égaux.
• Le triangle isocèle possède un axe de symétrie qui passe par son sommet principal et qui est la médiatrice de la base principale.

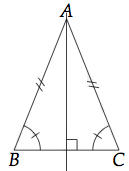
Dans le triangle ci-dessus, les angles ABC et ACB sont égaux

Je vous explique dans une partie suivante ce qu'est plus généralement la médiatrice d'un côté d'un triangle.

Triangle équilatéral

Le triangle équilatéral. Décortiquons le mot "équilatéral". Il est composé de "équi" qui signifie "égal" et de "latéral" qu'on pourrait traduire en "côté". Donc, un triangle équi-latéral est ... ?

Définition

Triangle équilatéral

Un triangle équilatéral est un triangle qui possède trois côtés de même longueur.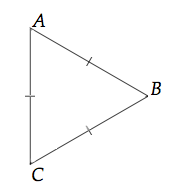




Dans le triangle ci-dessus, les trois côtés du triangle ABC, à savoir [AB], [AC] et [BC], sont égaux.

Donc cette fois-ci, trois angles égaux pour le triangle équilatéral. Et les angles ? Il sont sans doutes les trois égaux. Et réfléchissons : si la somme des angles d'un triangle est égale à 180° et que les trois angles d'un triangle équilatéral sont égaux, que valent-t-il ?

Propriétés

Propriétés du triangle équilatéral

Deux propriétés importantes sur les triangles équilatéraux :

• Les trois angles d'un triangle équilatéral sont égaux et valent 60°.
• Un triangle équilatéral possède 3 axes de symétries, chacun de ces axes passe par un sommet et est la médiatrice du côté opposé au sommet.

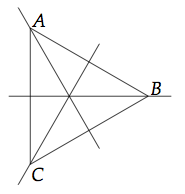
Dans le triangle ci-dessus, les angles 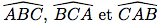sont égaux.

En effet, pour les angles :

Je reviendrai dans la suite de ce cours sur la notion de médiatrice.

Triangle rectangle

Je crois que le triangle rectangle, vous le connaissez déjà, non ?

Définition

Triangle rectangle

Un triangle rectangle est un triangle qui possède un angle droit.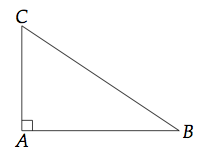




Dans le triangle ci-dessus, le côté [BC] du triangle ABC est appelé l'hypoténuse du triangle. De plus, on dit que le triangle ABC est rectangle en A.

L'hypoténuse est en fait le côté opposé à l'angle droit du triangle rectangle.

Le triangle rectangle aussi a des propriétés bien à lui. Les voici.

Propriétés

Ces propriétés sont logiques.
La seconde : encore une fois, si la somme des trois angles d'un triangle est égale à 180° et que le triangle rectangle possède un angle droit (90°), la somme des deux autre vaut :

De plus, dans un triangle rectangle, l'hypoténuse sera toujours toujours (je me répète exprès) le plus grand des côtés du triangle rectangle. C'est le principe de l'inégalité triangulaire que je vous explique dans la partie suivante.