Propriétés du produit scalaire

Elles sont nombreuses, et doivent toutes être comprises et connues par coeur.

Propriété

Coordonnées et produit scalaire

Soient de coordonnées (x,y) et de coordonnées (x',y') dans la base orthonormale .
Alors :

. = xx' + yy'

On additionne les produits des coordonnées deux à deux.

Exemple

Soient deux vecteurs (3, -4) et (0, 3).
Alors :

. = 3 × 0 + (-4) × 3 = -12

Et maintenant, avec un réel.

Propriétés

Propriétés du produit scalaire

Soient , et 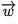trois vecteurs du plan et λ un réel.
On a les relation suivantes :

• Commutativité du produit scalaire :
  
  . = .


• Distribution :
  
  .( + ) = . + .


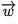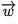
• Multiplication par un réel :
  
  .(λ) = λ(.)

Tout cela paraissait évident, non ?

Alors continuons avec ces évidences.

Propriétés

Identités remarquables et produit scalaire

Soient et deux vecteurs du plan.
On a les relations suivantes :

Ce ne sont que des vulgaires identités remarquables. Rien de plus, rien de moins.

Allez maintenant, appliquons tout cela !