Toutes les propriétés sur les parallélogrammes sont à connaître sur le bout des doigts. C'est pour cela que, dans ce cours, je vous rappelle la définition du parallélogramme, ses propriétés, ainsi que celles des parallélogrammes particuliers : carré, rectangle, losange, etc.
Définition et propriété d'un parallélogramme
Commençons par rappeler la définition d'un parallélogramme.
Définition
Parallélogramme
Un parallélogramme est un quadrilatère dont les côtés sont parallèles deux à deux.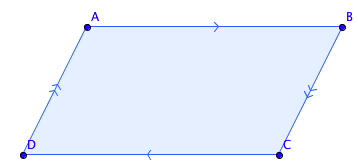
A partir du moment où un quadrilatère a ses quatre côtés parallèles, deux à deux, c'est un parallélogramme. Facile, non ?
On attaque les propriétés maintenant.
Propriétés
Propriétés du parallélogramme
Un parallélogramme possède les propriétés suivantes :- Ses côtés sont égaux deux à deux,
- Ses côtés sont parallèles deux à deux,
- Ses angles opposés sont égaux deux à deux,
- Ses diagonales se coupent en leur milieu.
On le voit très bien sur la figure ci dessous.
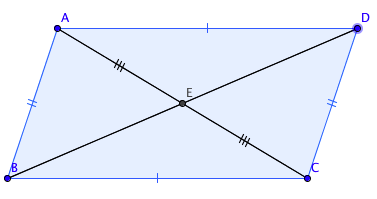
Si vous êtes devant une figure qui possède une de ses quatre propriétés précédentes, alors vous pourrez affirmez que c'est un parallélogramme.
Carré
Voyons à présent les figures géométriques qui sont des parallélogramme et commençons par le carré.
Définition
Carré
Un carré est un parallélogramme.Un carré possède quatre angles droits, quatre côtés sont égaux et parallèles deux à deux.
Ses diagonales ont la même longueur et se coupent en leur milieu.
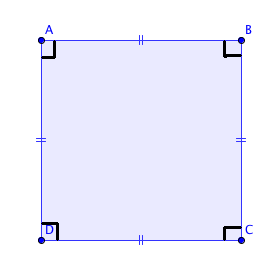
Si vous rencontrez un quadrilatère qui a ses diagonales de même longueur, alors c'est un carré.
Rectangle
Le rectangle également.
Définition
Rectangle
Un rectangle est un parallélogramme.Un rectangle possède quatre angles droits, ses côtés sont parallèles et égaux deux à deux.
Ses diagonales sont égales et se coupent en leur milieu.
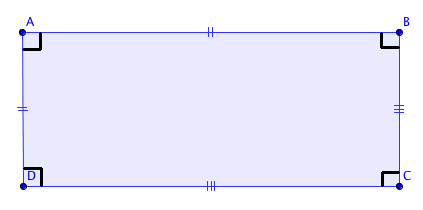
Si vous avez un parallélogramme, c'est un rectangle s'il possède un angle droit, ou si ses diagonales ont la même longueur.
Losange
Enfin, on se rappelle tous que le losange aussi est un parallélogramme.
Définition
Losange
Un losange est un parallélogramme.Un losange possède quatre côtés égaux et parallèles deux à deux.
Ses diagonales sont perpendiculaires et se coupent en leur milieu.
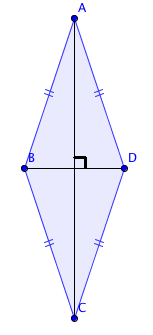
Si vous avez un parallélogramme, c'est un losange s'il possède deux côtés consécutifs de même longueur, ou si ses diagonales sont perpendiculaires.
On répéte, si vous rencontrez un quadrilatère qui :
- - A ses diagonales de même longueur, alors c'est un carré,
- - Possède trois angles droits, alors c'est un rectangle,
- - Possède quatre côtés de même longueur, alors c'est un losange.
Quelques exercices sur Parallélogrammes :