Des petits rappels de première S sur le produit scalaire dans le plan avant d'attaquer les mêmes notions mais dans l'espace.
1 - Définitions du produit scalaire
Je vais vous (re)définir tout d'abord cette notion.
Définition
Produit scalaire
Soient
et 
deux vecteurs du plan.
Le produit scalaire de
et est un réel, que l'on note ., défini par :
- Si ≠ 0 et ≠ 0 :
. = ||||.||||.cos(, ) - Si et sont nuls :
. = 0
La notation |||| signifie la norme du vecteur .
En réalité, ce n'est que le produit de la norme de et de la norme de que l'on multiplie par le cosinus de l'angle formé par ces deux vecteurs.
Si les deux vecteurs sont nuls, biensur leurs normes sont nulles, et donc leur produit scalaire aussi.
Remarque
. se note ² et est appelé carré scalaire.
Exemple
et avec |||| = 3, |||| = 4 et l'angle formé par ces deux vecteurs vaut 
soit 30°.
Calculons le produit scalaire de ces deux vecteurs.
. = ||||.||||.cos(, ) = 3 × 4 × cos()Or, cos(
) = 
, tout le monde le sait.
. = 3 × 4 × cos() = 12 × = 
Le produit scalaire, comme je vous l'ai dit en introduction, permet de démontrer l'orthogonalité de deux vecteurs.
Définition
Orthogonalité et produit scalaire
Soient et deux vecteurs du plan.
Si
. = 0, alors les vecteurs et sont orthogonaux.
Cela se voit très bien regardez.
Démonstration : Si le produit scalaire est nul, c'est soit que la norme de est nulle, soit que celle de est nulle, soit que le cosinus de l'angle formé par ces deux vecteurs est nul.
Or, si les normes des deux vecteurs étaient nulles, les vecteurs seraient forcément nul.
Donc, cela ne peut qu'être le cosinus qui soit nul.
Mais un angle de
, c'est un angle droit !
Terminé.
Quand on fait le produit scalaire de deux vecteurs, c'est en fait une projection orthogonale de l'un sur l'autre.
Propriété
Propriété du produit scalaire
Soient A,B et C trois points distincts du pal, et H le projeté orthogonal de C sur (AB).
- Si
et 
sont de même sens :
= AB × AH - Si et sont de sens opposés :
= -AB × AH
Tout est très clair, je n'ai rien à ajouter là dessus.
Passons à présent aux propriétés relatives au produit scalaire.
2 - Propriétés du produit scalaire
Elles sont nombreuses, et doivent toutes être comprises et connues par coeur.
Propriété
Coordonnées et produit scalaire
Soient de coordonnées (x,y) et de coordonnées (x',y') dans la base orthonormale 
.
Alors :
. = xx' + yy'On additionne les produits des coordonnées deux à deux.
Exemple
(3, -4) et (0, 3).
Alors :
. = 3 × 0 + (-4) × 3 = -12Et maintenant, avec un réel.
Propriétés
Propriétés du produit scalaire
Soient, et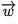 
trois vecteurs du plan et λ un réel.
On a les relation suivantes :
- Commutativité du produit scalaire :
. = . - Distribution :
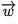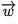
.( + ) = . + . - Multiplication par un réel :
.(λ) = λ(.)
Tout cela paraissait évident, non ?
Alors continuons avec ces évidences.
Définition
Identités remarquables et produit scalaire
Soient et deux vecteurs du plan.
On a les relations suivantes :
Ce ne sont que des vulgaires identités remarquables. Rien de plus, rien de moins.
Allez maintenant, appliquons tout cela !
3 - Applications du produit scalaire dans le plan
Plusieurs théorèmes célèbres sont issus de ce produit scalaire. Et oui, on ne fait rien qui ne sert à rien !a - Théorème de la médiane
Théorème
Théorème de la médiane
Soient A et B deux points distincts du plan et I le milieu de [AB].
Pour tout point M du plan, on a les relations suivantes :
Exemple
Rien de plus simple, on applique tout bêtement.
b - Thorème d'Al Kashi
Vous connaissiez Pythagore en 4ème, mais son théorème n'est qu'un cas particulier de celui d'Al Kashi que je vais vous montrer tout de suite.
Théorème
Théorème D'Al Kashi
Soit un triangle ABC avec AB = c, AC = b et BC = a.
On a les relations suivantes :
Rappelez-vous, pour appliquer le théorème de Pythagore, il nous faut un triangle rectangle, soit un angle droit, un angle de .
Et le cosinus d'un angle droit vous combien ? Il est nul.
Donc, si l'angle droit est en A, les formules se transforment en : a² = b² + c²
C'est le théorème de notre cher Pythagore, oui.
Grâce à ce théorème, en particulier, vous saurez calculer tous les angles d'un triangle en ayant juste la longueur de ces côtés. Tiens ! Faites-le.
c - Formule des sinus
Après les cosinus, les sinus ! Le produit scalaire nous donne des propriétés sur les sinus.
Propriété
Formule des sinus
Soit un triangle ABC d'aire
avec AB = c, AC = b et BC = a.
On a les relations suivantes :
Un nouvelle façon de calculer l'aire d'un triangle sans utilisée la base et la hauteur.
Exemple
= 30° et 
= 60°.
Calculer le côté [AC].
Pour trouver b, on utilise la relation :
Or,
Donc :
d - Distance d'un point à une droite
Je vais vous apprendre à calculer la distance d'un point du plan à une droite.
Propriété
Distance d'un point à une droite
Soient
la droite d'équation ax + by + c = 0, avec a et b non nuls, et A(xA; yA) un point du plan.
La distance du point A à la droite
est la distance AH, avec H le projeté orthogonal de A sur .
On a :
C'est la fractions avec au numérateur les coordonnées du point A dans l'équation de la droite , et au dénominateur les coefficient a et b de l'équation de la drotie élevés au carré sous la racine.
N'ayez pas peur des valeurs absolues au numérateur, elle sont là pour que le tout soit positif, car une distance est toujours positive.
Exemple
la droite d'équation 4x + 5y - 1 = 0 et A(4; 0) un point du plan.
La distance de A à
est donc la distance AH, avec H le projeté orthogonal de A sur .
e - Equations et produit scalaire
Deux propriétés sur les équations et l'on aura terminé pour ce chapitre.
Propriété
Equations et produit scalaire
- La droite orthogonale à
passant par A est :
- Le cercle de diamètre [AB] est :
Le premier ensemble fait référence à la définition du produit scalaire suivante : si le produit scalaire de deux vecteurs est nul alors ces vecteurs sont orthogonaux.
La seconde fait référence à un triangle dans un cercle dont l'un des côtés est diamètre de ce cercle, ce triangle est forcément rectangle. Et bien ici, si les vecteurs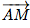 
et 
sont orthogonaux, cela signifie que le segment [AB] est diamètre d'un cercle.