Dans ce cours, je vous apprends, étape par étape comment démontrer qu'une suite numérique est géométrique en trouvant la raison et son premier terme.
Considérons la suite numérique un suivante :
∀ n ∈ N, un+1 = 3un - 1
Ainsi que la suite vn définie par :
Dans ce cours méthode, je vais vous montrer comment démontrer que vn est géométrique.
Rappelons tout d'abord la définition d'une suite géométrique.
Définition
Suite géométrique
On appelle suite géométrique de premier terme u0 et de raison q la suite définie par :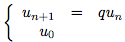
Exprimer vn+1 en fonction de vn
Pour tout entier naturel n, calculons vn+1.
Il faudra faire apparaître l'expression de vn dans le résultat pour pouvoir exprimer vn+1 en fonction de vn.
En effet, nous cherchons à obtenir un résultat qui soit de la forme : vn+1 = vn × q, avec q ∈ R (c'est la raison de suite géomtrique, vous l'aurez compris).
Calculons donc vn+1 :
vn+1 = 2 × (3un - 1) - 1
vn+1 = 6un - 2 - 1
vn+1 = 6un - 3
Exprimons maintenant vn+1 en fonction de vn.
On sait que :
Donc, ∀ n ∈ N :
| un = | vn + 1 |
|---|---|
| 2 |
Ainsi, ∀ n ∈ N :
| vn+1 = 6 | vn + 1 | - 3 |
|---|---|---|
| 2 |
vn+1 = 3 × (vn + 1) - 3
vn+1 = 3vn + 3 - 3
vn+1 = 3vn
Conclure que la suite vn est géométrique
Rappellons tout d'abord la condition pour qu'une suite soit géométrique : si ∀ n ∈ N, vn+1 = vn × q, avec q ∈ R, alors vn est une suite géométrique.
On précise la valeur de sa raison q et de son premier terme v0.
Attention
Pour tout entier n, on a vn+1 = 3vn.
Donc vn est une suite géométrique de raison q = 3 et de premier terme :




