Suite géométrique

Cours première ES

Une autre catégorie de suite à présent, les suites dites géométriques.

Définition

Suite géométrique

On appelle suite géométrique de premier terme u₀ et de raison q la suite définie par :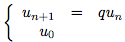

Puis-je avoir une définition concrète pour cette catégorie de suite aussi s'il-vous-plaît ?

Si c'est demandé si poliment.

Exemple

Soit la suite numérique u_n définie par :



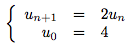
Cette suite est une suite géométrique de raison 2.
Si l'on calcule les cinq premiers termes de cette suite,

u₀ = 4
u₁ = 2 × u₀ = 2 × 4 = 8
u₂ = 2 × u₁ = 2 × 8 = 16
u₃ = 2 × u₂ = 2 × 16 = 32
u₄ = 2 × u₃ = 2 × 32 = 64

Que remarquez-vous ici ?
Le quotient de deux termes consécutifs est constant et égal à la raison 2. On multiplie de 2 à chaque u_n suivant.

Il existe aussi des propriétés pour calculer le 1000^ème terme sans passer par les 1000 premiers.

Propriétés

Exemple

Il y a également une formule pour calculer la somme de tous les termes d'une suite géométrique. La voici.

Propriété

Somme des termes d'une suite géométrique

Soit u une suite géométrique.
La somme des termes de cette suite est donnée par :

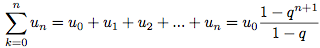
Vous pouvez aussi réutilisez directement cette formule. Mais il faut que vous la compreniez aussi bien que la précédente pour les suites arithmétiques.

Exemple

Soit la suite numérique u_n définie par :



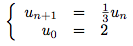
Cette suite est géométrique de raison 1/3.
Calculons la somme des 100 premiers termes de cette suite.



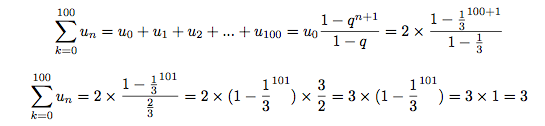
La quantité est tellement réduite que .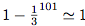
On peux vous demander de calculer la somme de tous les termes de la suite u_n en fonction de n. C'est pareil, sauf qu'on laisse le n tel quel.

Remarque

On peut vous demander de montrer qu'une suite v_n définie en fonction d'une autre suite (u_n) est géométrique.
Dans ce cas, Il suffit de montrer qu'il existe q ∈ * tel que v_{n + 1} = qv_n.

Je vais vous donner un exemple pour vous montrer les directives à suivre.

Exemple

Soit la suite numérique u_n définie par :



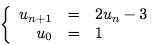
Nous allons montrer que la suite v_n = u_n - 3 est géométrique.
Il suffit donc de montrer qu'il existe q ∈ * tel que v_{n + 1} = qv_n.
On part toujours de v_{n + 1},

v_{n + 1} = u_{n + 1} - 3 = 2u_n - 3 - 3 = 2u_n - 6

On a utilisé la formule v_{n + 1} = u_{n + 1} - 1 et remplacé les n par des n + 1.

v_n = u_n - 1

Or :

v_n = u_n - 3 ⇔ u_n = v_n + 3

Donc :

v_{n + 1} = 2u_n - 6 = 2(v_n + 3) - 6 = 2v_n + 6 - 6 = 2v_n

Conclusion : v_n est une suite géométrique de raison q = 2 et de premier terme :

v₀ = u₀ - 3 = 1 - 3 = -2

On peut alors écrire la chose suivante :

v_n = (-2) × 2ⁿ