-
Déterminer une équation du plan P passant par A(-1; 2; 4), B(3; 0; 5) et C(-8; 6; 2).
Les vecteurs
(4; -2; 1) et 
(-7; 4; -2) ne sont pas colinéaire, cela se voit facilement.
Soit
(a; b; c) un vecteur normal au plan (ABC) et essayons de déterminer ses coordonnées possibles.
. = 0 et . = 0 ⇔ 4a - 2b + c = 0 et -7a + 4b - 2c = 0
Prenons c = 1.
On obtient le vecteur normal au plan (ABC) suivant :
(0; 0,5; 1).
Soit M(x; y; z) un point de l'espace.
M(x; y; z) ∈ (ABC) ⇔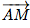 
. = 0
⇔ 1 (y - 2) + (z - 4) = 0 2
⇔ y + 2z - 10 = 0 -
Déterminer une équation du plan P' contenant le point D(1; 1; 2) et perpendiculaire au plan (ABC).
Notons
'(a'; b'; c') un veceur normal au plan P'.
On a.' = 0.
Donc :
1 y' + c' = 0 2
On peut prendre'(1; 2; -1).
P' a une équation du type :
x + 2y - z + d = 0.
Comme D(1; 1; 2) est un point de P', on a :
d = -1
D'où l'équation de P' suivante :
x + 2y - z - 1 = 0