On considère trois points de l'espace A(2; 0; 0), B(0; 4; 0) et C(0; 0; 5).
-
Déterminer une équation cartésienne du plan (ABC).
Il nous faut d'abord trouver un vecteur normal au plan (ABC).
On trouve aisément les coordonnées des vecteurs
et 
qui sont : (-2; 4; 0) et (-2; 0; 5).
Soit
(a; b; c) le vecteur normal recherché.
. = 0 et . = 0 ⇔ -2a + 4b = 0 et -2a + 5c = 0
⇔ a = 2b et a = 5c/2
Prenons donc, par exemple,(10; 5; 4). Ce vecteur vérifie bien les équations précédentes.
On peut maintenant déterminer une équation du plan (ABC).
Soit M(x; y; z) un point de l'espace.
M(x; y; z) ∈ (ABC) ⇔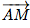 
. = 0
⇔ 10x + 5y + 4z - 20 = 0 -
Déterminer les coordonnées du points H, projeté orthogonal de O, origine du repère, sur le plan (ABC).
Les vecteurs
et sont colinéaires. Forcément, car tous les deux sont orthogonaux au plan (ABC).
Donc, il existe un réel λ tel que :
= λ.
Si on reprant les coordonnées du vecteur, on a :
H(10λ; 5λ; 4λ)
Or, le point H appartient au plan (ABC).
Donc, il vérifie son équation (celle trouvée dans la question précédente).
10(10λ) + 5(5λ) + 4(4λ) - 20 = 0
On obtient alors :
λ = 20 141
D'où :
H( 200 ; 100 ; 80 ) 141 141 141 -
Démontrer que H est l'orthocentre du triangle ABC.
On calcule facilement les coordonnées du vecteur
qui sont :
(200 ; 100 ; -625 ) 141 141 141
Et on a('-2; 4; 0).
Donc :
. = 0
De même :
.
= 0
On en déduit que H est l'orthocentre du triangle ABC.