Terminons ce cours sur le produit scalaire par ses applications en géométrie. Parmi elles, je vous apprends deux théorèmes : celui de la médiane et le théorème d'Ali Kashi. Mais aussi une formule des sinus et deux propriétés sur les équations et produit scalaire.
Plusieurs théorèmes célèbres sont issus de ce produit scalaire. Et oui, on ne fait rien qui ne sert à rien !
1 - Théorème de la médiane
Théorème
Théorème de la médiane
Soient A et B deux points distincts du plan et I le milieu de [AB].
Pour tout point M du plan, on a les relations suivantes :
Exemple
Rien de plus simple, on applique tout bêtement.
2 - Théorème d'Al Kashi
Vous connaissiez Pythagore en 4ème, mais son théorème n'est qu'un cas particulier de celui d'Al Kashi que je vais vous montrer tout de suite.
Théorème
Théorème D'Al Kashi
Soit un triangle ABC avec AB = c, AC = b et BC = a.
On a les relations suivantes :
Rappelez-vous, pour appliquer le théorème de Pythagore, il nous faut un triangle rectangle, soit un angle droit, un angle de 
.
Et le cosinus d'un angle droit vous combien ? Il est nul.
Donc, si l'angle droit est en A, les formules se transforment en : a² = b² + c²
C'est le théorème de notre cher Pythagore, oui.
Grâce à ce théorème, en particulier, vous saurez calculer tous les angles d'un triangle en ayant juste la longueur de ces côtés. Tiens ! Faites-le.
3 - Formule des sinus
Après les cosinus, les sinus ! Le produit scalaire nous donne des propriétés sur les sinus.
Propriété
Formule des sinus
Soit un triangle ABC d'aire
avec AB = c, AC = b et BC = a.
On a les relations suivantes :
Un nouvelle façon de calculer l'aire d'un triangle sans utilisée la base et la hauteur.
Exemple
= 30° et 
= 60°.
Calculer le côté [AC].
Pour trouver b, on utilise la relation :
Or,
Donc :
4 - Equations et produit scalaire
Deux propriétés sur les équations et l'on aura terminé pour ce chapitre.
Propriété
Equations et produit scalaire
- La droite orthogonale à
passant par A est :
- Le cercle de diamètre [AB] est :
Le premier ensemble fait référence à la définition du produit scalaire suivante : si le produit scalaire de deux vecteurs est nul alors ces vecteurs sont orthogonaux.
La seconde fait référence à un triangle dans un cercle dont l'un des côtés est diamètre de ce cercle, ce triangle est forcément rectangle. Et bien ici, si les vecteurs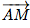 
et 
sont orthogonaux, cela signifie que le segment [AB] est diamètre d'un cercle.